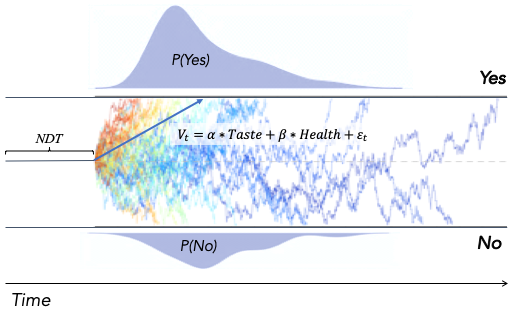
Fitting the Drift Diffusion Model
Now that you've gotten familiar with some of the basic parameters of the DDM, and how they relate to choice and RTs, you may want to start using the DDM to make inferences about parameters in your own data, and from there, make inferences about psychological theories. For example, imagine that you are doing a study on altruistic choice and you want to know whether people's intuitive response is to be selfish or to be generous. So you put them under time pressure, and lo and behold, not only do their RTs become shorter, but they also become more generous! Is this good evidence that people's intuitive response is to be generous? Not so fast (irony intended)...
As we've seen, a lot of different parameters can influence how quickly someone responds, and what kinds of choices they make. This can include the drift rate, the threshold, starting biases, etc. And we've seen how complex those changes can be to interpret when just looking at simple statistics like mean RT or mean acceptance rate.
This is where model-fitting comes in. In essence, we want to ask, "What parameters best explain the full pattern of choices and RTs that I observe in my data?" There are many ways to answer this question, and whole tomes have been written on the "best" way to estimate these parameters (e.g., Ratcliff et al., 2002; Vanderkerckhove et al., 2007). Luckily, over the last few years, a number of methods and software packages have been developed to help with fitting the DDM to experimental data.
Here are some of the most widely and/or easily used packages:
The EZ-Diffusion Model: Useful if you have a large number of observed choices and RTs for a single condition (i.e., where you assume that the drift rate, threshold, and non-decision time parameters are the same for every observed trial). For example, if you have 200 trials in which people categorize facial expressions as angry or neutral, and the only difference is whether the person expressing the emotion is black or white, you could potentially use this website to calculate the drift rate, threshold, and non-decision time for each condition (i.e. black-angry, black-neutral, white-angry, white-neutral) to see if race alters the process of evidence construction.
Hierarchical Drift-Diffusion Model: This has become the real workhorse of the DDM community. It's a relatively easy-to-use package written in Python that has many advantages. It essentially treats estimation of DDM parameters like a mixed-effects regression problem, meaning that you can have fewer trials per subject and still get decent estimates. You can also examine how trial-by-trial changes in some experimental variable of interest (e.g., neural signals, perceptual or subjective value evidence, etc.) influence the choice process. The only downside here is that this package currently only estimates the canonnical form of the DDM, which assumes that the value of parameters does not change within a trial. If you are interested in dynamics problems (e.g. ones where you assume the evidence might change over the course of a few hundred milliseconds (as dual-process models might) then hDDM won't really work for you.
Differential evolution DDM: This approach, developed very recently by Holmes & Trueblood (2018) and written in MATLAB, is perhaps the most flexible toolkit currently available. It works similarly to the hDDM package, using Bayesian updating methods to find good-fitting parameter estimates. However, it also allows the user to specify whatever kind of DDM they would like, including DDMs that have time-varying evidence or collapsing bounds. As long as the user is able to specify an algorithm for estimating the likelihood of the data for a given set of parameter values, this set of scripts should work to estimate those parameters. This is currently the approach that most of the work in my lab is taking.
Using the packages listed above requires some basic familiarity with the logic of model-fitting. Below, you can find some code examples and references that you can use to help you learn about many of these basic model-fitting approaches.
Model-fitting: Basics
Coming soon!
In the mean-time, check out this book if you want to learn more.
Model-fitting: Maximum Likelihood Methods
Coming soon!
Model-fitting: Chi-square and Simplex Methods
Coming soon!
Model-fitting: Bayesian Methods
Coming soon! In the meantime, I highlighly recommend these two books:
-
Doing Bayesian Data Analysis by John Kruschke
-
Bayesian Cognitive Modeling by Lee & Wagenmakers.
Return to home page.
References
Holmes, W. R., & Trueblood, J. S. (2018). Bayesian analysis of the piecewise diffusion decision model. Behavior Res. Methods, 50(2), 730-743.
Ratcliff, R., & Tuerlinckx, F. (2002) Estimating parameters of the diffusion model: Approaches to dealing with contaminant reaction times and parameter variability. Psychonomic Bull. Rev., 9, 438-481.
Vandekerckhove, J., & Tuerlinckx, F. (2007). Fitting the Ratcliff diffusion model to experimental data. Psychonomic Bull. Rev., 4, 1011-1026.